🔗 문제
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr











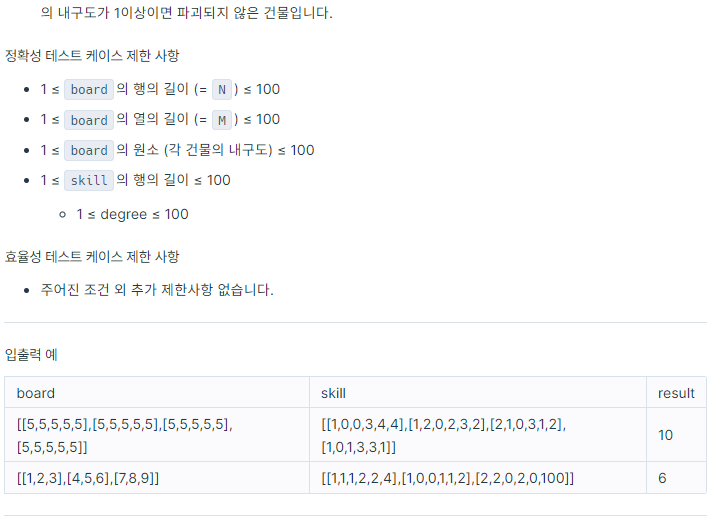
👨🏻💻 풀이 및 코드
시도 1 - 브루트포스 (시간초과)
단순히 완탐으로 스킬에 포함되는 구간만큼 내구도를 높이거나 낮추는 작업을 하면 시간 초과가 발생합니다.
이 때의 시간 복잡도는 세로의 길이를 N, 가로의 길이가 M, 스킬의 갯수가 K개 일때
O(N * M * K)
의 시간 복잡도를 가집니다.
누적합을 사용하여, 스킬을 사용할 떄마다 N*M 크기만큼 배열을 도는 것이 아니라 O(1) 만에 해결할 수 있습니다.
시도 2 - 누적 합 (성공)
1) 1차원 누적합
- 만약 [1, 2, 3, 4, 5] 에서 0번인덱스부터 3번 인덱스까지 2를 더해주고 싶다면 [2, 0, 0, 0, -2] 라는 새로운 배열을 생성합니다.
- 그 후에 이 새로운 배열을 0번인덱스부터 마지막 인덱스까지 차례대로 현재 인덱스에 이전 값을 더해주면 [2, 2, 2, 2, 0] 이라는 배열이 생성됩니다. 이 누적합된 배열과 기존의 [1, 2, 3, 4, 5] 배열을 더해주면 [3, 4, 5, 6, 7, 5] 라는 구하려고 하는 배열의 형태가 됩니다.
- 즉, 누적합을 통해 원하는 배열을 만들기 위해 1차원 배열에서 변화시키려는 구간이 a ~ b 구간이고 c의 변화를 주려면 새로운 배열에 a 번째 원소에 c를 더하고, b+1 번째 원소에 -c를 빼준 후 누적합 시키면 됩니다.
- 이와 같은 방식을 사용하면 O(1)의 시간복잡도로 처리가 가능합니다.
이제 2차원으로 적용해봅시다.
2) 2차원 누적합
만약, 다음과 같이 구간 (1, 1) 와 (2, 2) 사이에 5를 더하고 싶다면, (1, 1) = 5, (1, 2+1) = -5, (2+1, 1) = -5, (2+1, 2+1) = 5 를 각각 대입한 후, 상하 방향으로 합산, 그 결과를 좌우 방향으로 합산하면 원하는 배열을 구할 수 있습니다.
상하 방향의 합산
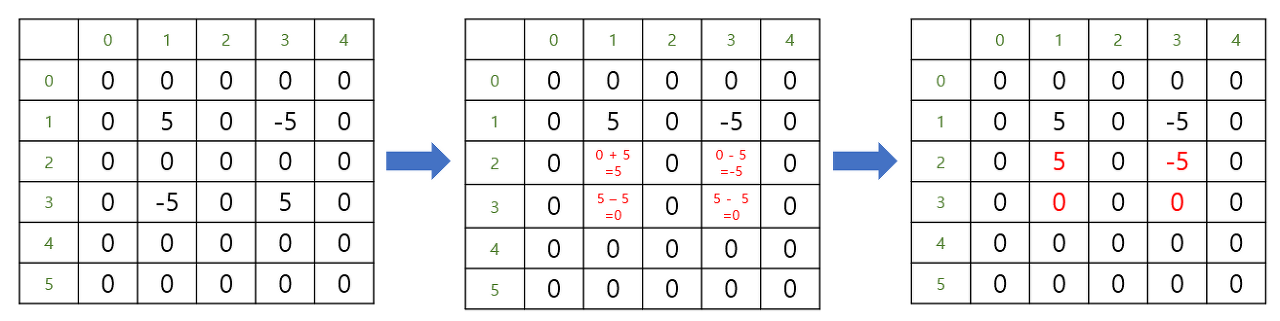
상하 방향의 합산 결과를 좌우 방향 합산
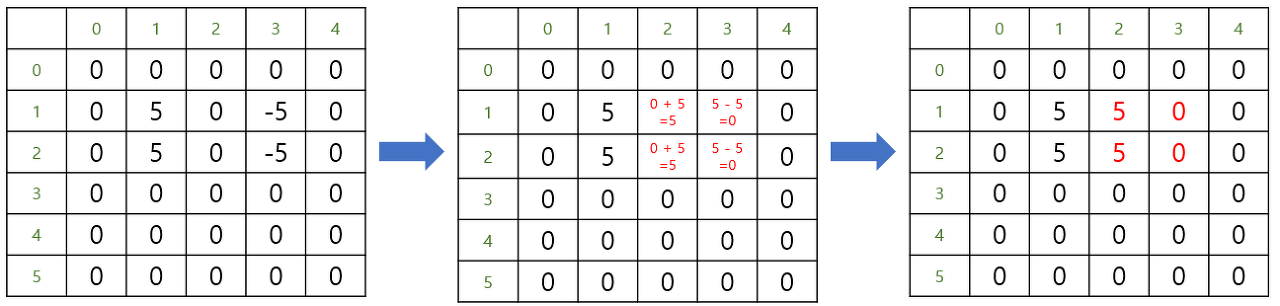
(출처 : https://jangcenter.tistory.com/121)
총 시간 복잡도 : O(N*M)
전체 코드
import java.util.*;
class Solution {
public int solution(int[][] board, int[][] skill) {
int answer = 0;
int n = board.length;
int m = board[0].length;
int[][] sum = new int[n+1][m+1];
//각 구간 표시 O(k) (k:skill의 갯수)
for(int[] s : skill) {
int degree = (s[0] == 1) ? s[5]*-1 : s[5]; //type이 1이면 내구도를 낮춘다.
int r1 = s[1], c1 = s[2];
int r2 = s[3], c2 = s[4];
sum[r1][c1] += degree;
sum[r1][c2+1] -= degree;
sum[r2+1][c1] -= degree;
sum[r2+1][c2+1] += degree;
}
//누적합 계산
//상->하 O(n*m)
for(int j=0; j<=m; j++) {
for(int i=1; i<=n; i++) {
sum[i][j] += sum[i-1][j];
}
}
//좌->우 O(n*m)
for(int i=0; i<=n; i++) {
for(int j=1; j<=m; j++) {
sum[i][j] += sum[i][j-1];
}
}
//최종 내구도 계산 O(n*m)
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(board[i][j] + sum[i][j] > 0) answer++;
}
}
return answer;
}
}'알고리즘 풀이 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 기둥과 보 설치 - JAVA (0) | 2023.09.20 |
|---|---|
| [프로그래머스] 길 찾기 게임 - JAVA (0) | 2023.09.19 |
| [프로그래머스] 풍선 터트리기 - JAVA (0) | 2023.08.04 |
| [프로그래머스] 당구 연습 - JAVA (0) | 2023.06.28 |
| [프로그래머스] 방의 개수 - JAVA (0) | 2023.06.08 |



