🔗 문제
10986번: 나머지 합
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오. 즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j)
www.acmicpc.net
💻 풀이 및 코드
문제 유형 : 수학, 누적합
주어진 배열 중 구간(i, j) 합 이 M 으로 나누어 떨어져는 구간의 갯수를 구하는 문제
풀이
- 시간 복잡도 : O (N)
문제를 풀기 앞서, 아래의 모듈러 연산의 분배 법칙을 알고 있어야 한다.

문제에 나와있는 '연속된 부분 구간의 합이 M 으로 나누어 떨어지는' 이라는 의미를 생각해보자.
어떠한 구간 [a, b] 에 대해 '[a, b] 구간합 == [1, b] 구간합 - [1, a-1] 구간합' 임은 당연하다.
arr[x] 를 '[1, x] 의 구간합' 이라고 정의하자. 그렇다면 '연속된 부분 구간의 합이 M 으로 나누어 떨어진다' 라는 말을 수식으로 적어보면 '(arr[b] - arr[a-1])%M == 0' 이 된다. 이는 분배 법칙에 따라 다음과 같이 정의할 수 있다.

이때, 우변이 0이므로 좌변도 0이다. 따라서 구간 [a, b] 에 대해 'arr[b] % M == arr[a-1] % M' 이라면 [a, b] 의 구간합은 M 으로 나누어 떨어진다.
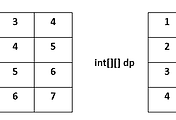
예제 입력 1을 생각해보자.
5 3
1 2 3 1 2
1. x = 1

이 때 문제의 조건을 만족하는 부분이 없다. answer = 0
2. x = 2

이 때에도 문제의 조건을 만족하는 부분은 없다. 하지만 x =2 인 조건 자체가 만족하므로 카운팅한다. answer = 1
3. x= 3

x = 2 일 때와 나머지가 동일하다. 따라서 answer = 2 가 되고, x = 2 일 때와 마찬가지로 자체적으로 0이므로 answer = 3 이 된다.
4. x = 4

x =1 과 나머지가 동일하다. 따라서 answer = 4 가 된다.
5. x = 5

x = 2 와 x =3 두 개의 구간과 나머지가 동일하다. 따라서 answer = 6 이 되고, 마찬가지로 나머지가 0 이므로 answer = 7 이 된다.
이런식으로 구간합을 구하고 하나씩 나머지가 같은 쌍을 구하면 O(n^2) 의 시간복잡도가 나온다.
이를 O(n) 으로 줄이기 위해 동일한 나머지의 갯수를 세는 시간 복잡도를 O(1) 으로 줄이자. 이것은 배열 cnt[1000] 을 생성해 갯수를 저장하여 사용하여 해결할 수 있다. (M 의 최대 범위 : 1000)
나머지는 코드를 보면 이해가 갈 것 같다.
전체 코드
import java.io.*;
import java.util.*;
public class Main_bj_10986_나머지합 {
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("res/input_bj_10986.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[] cnt = new int[1000]; // M의 최댓값은 1000, 나눈 나머지의 갯수를 세는 배열
long ans = 0;
int sum = 0;
st = new StringTokenizer(br.readLine(), " ");
while(N-- > 0) {
int num = Integer.parseInt(st.nextToken());
sum += num;
sum %= M;
ans += cnt[sum];
cnt[sum]++;
if(sum == 0) ans++;
}
System.out.println(ans);
br.close();
}
}Reference
[자바] 백준 10986 - 나머지 합 (java)
문제 : boj10986 필요 알고리즘 개념 수학, 누적 합 수학적 사고를 통해 어떻게 구할 수 있을지 생각할 수 있어야 한다. 내 경우엔 해당 풀이를 구현하기 위해 누적합 알고리즘을 사용했다. ※ 제 코
nahwasa.com
'알고리즘 풀이 > 백준' 카테고리의 다른 글
| [BOJ] 23290. 마법사 상어와 복제 - JAVA (0) | 2023.04.24 |
|---|---|
| [BOJ] 11660. 구간 합 구하기 5 - JAVA (0) | 2023.03.16 |
| [BOJ] 1912. 연속합 - JAVA (0) | 2023.03.13 |
| [BOJ] 6549. 히스토그램에서 가장 큰 사각형 (세그먼트 트리) (0) | 2023.03.06 |
| [BOJ] 11444. 피보나치 수 6 - JAVA (0) | 2023.03.03 |